今度は公園での「宝探し」を例に、3次元（空間）の測位を理解してみましょう。砂浜で掘り当てた宝箱の中には、次の宝につながるヒントが入っていました。

1） 公園には街灯（A地点）とすべり台（B地点）と水飲み場（C地点）があり、「街灯（A）から20ｍ」「すべり台（B）から12ｍ」「水飲み場（C）から15ｍ」と宝のありかのヒントが与えられました。

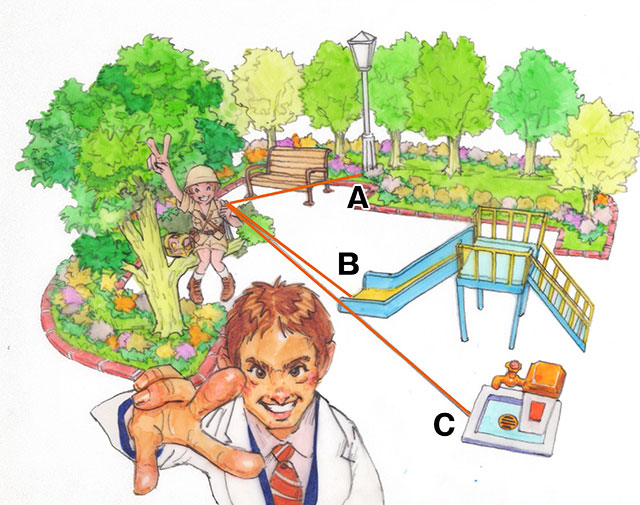
2） そこで、ロープを3本用意して、1本ずつそれぞれを結び、「街灯（A）から20ｍ」「すべり台（B）から12ｍ」「水飲み場（C）から15ｍ」のところに結び目が来るようにして3本のロープを結びました。

3） 結び目を持って歩き回り、3本ともピンと張る場所が見つかれば、そこが宝のありか、というわけです。

4） ところが歩き回ってもなかなか「3本とも」という場所が見つかりません。どの2本が張った状態でも、困ったことに残りの1本がゆるんでしまうのです。

5） 動き回りながら考えました。「結び目を高く持ち上げれば、3本ともピンと張る場所が見つかるかもしれない——」

6） さっそく公園の樹木に登ってみたら、ちょうど3本のロープがピンと張る場所で小さな宝箱が見つかりました。（地面の下にもピンと張る場所はあり得ますが、地中なので除外します。）

2次元（平面）の測位では2点からの距離でしたが、高さも含めた3次元の場合には「3点からの距離が決まる」ことで測位ができることが、分かってもらえたと思います。

監修：久保信明（東京海洋大学 大学院 准教授）、構成：喜多充成、イラスト：西井 匡